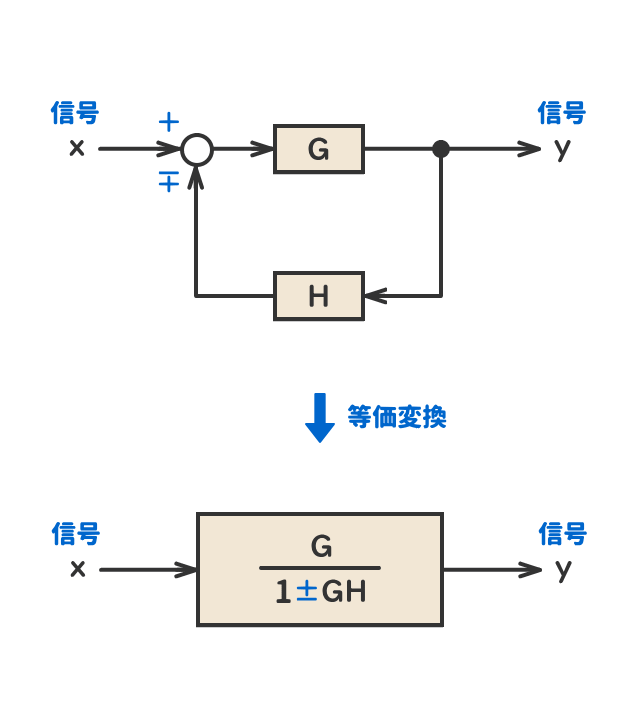
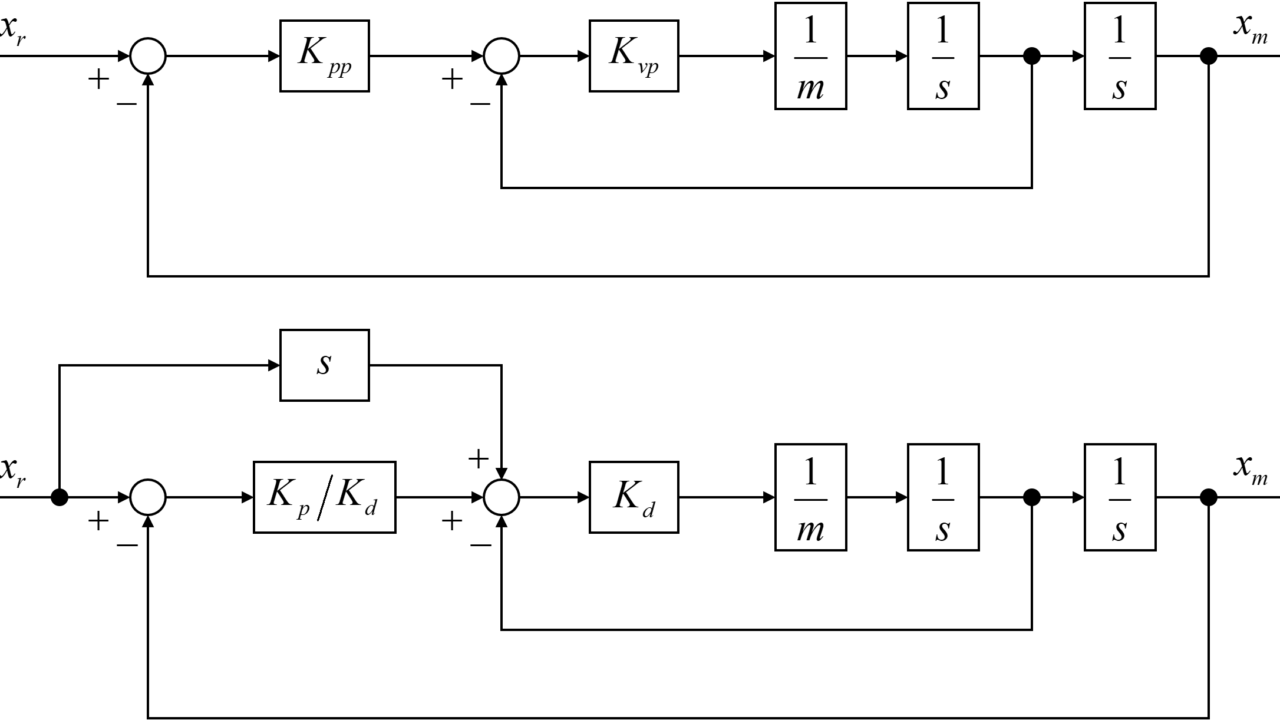
ブロック線図が複雑な場合、不必要な信号を消去し、簡略化する。 その等価変換の方法を表 1.4 に示す。 表 1.4: 問題図2.6 (c) 【解答】 (a) 1 ( +1)2 + + − −
ブロック線図を簡略化する:ブロック線図の特性を利用する方法|Tajima Robotics
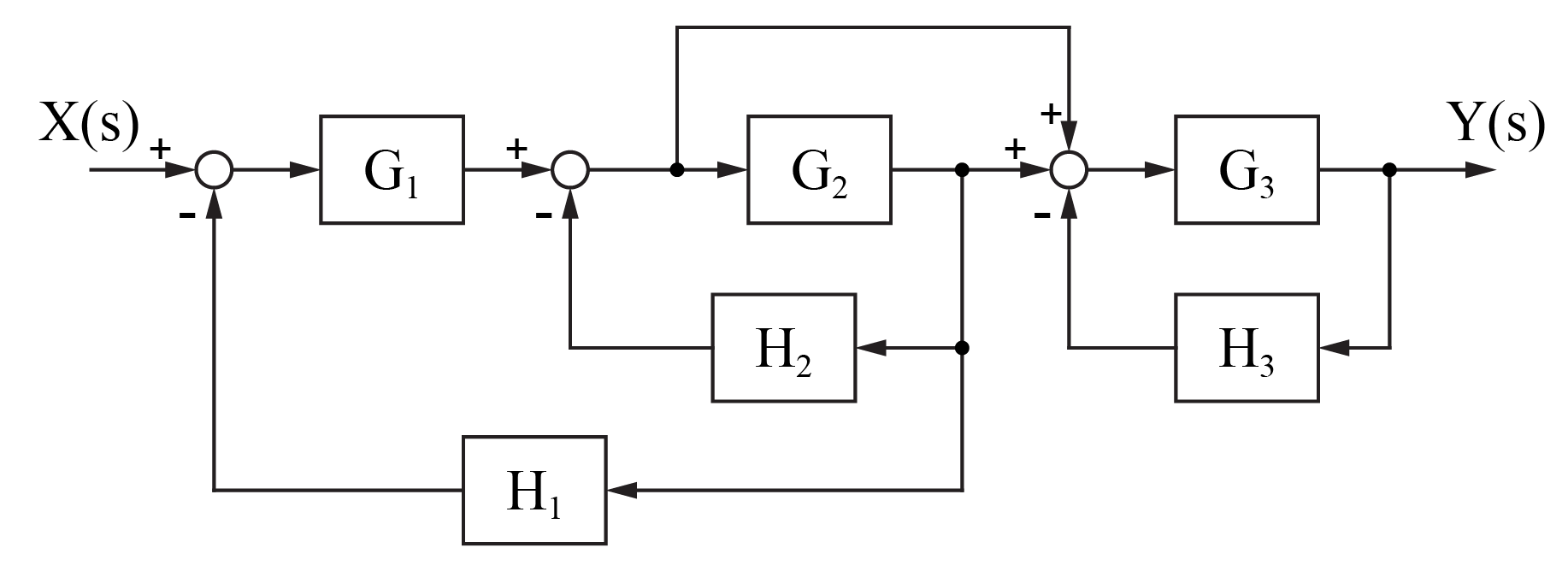
問題図2.6(a)~(c) のブロック線図を簡単化し, r からy までの伝達関数を求めよ.
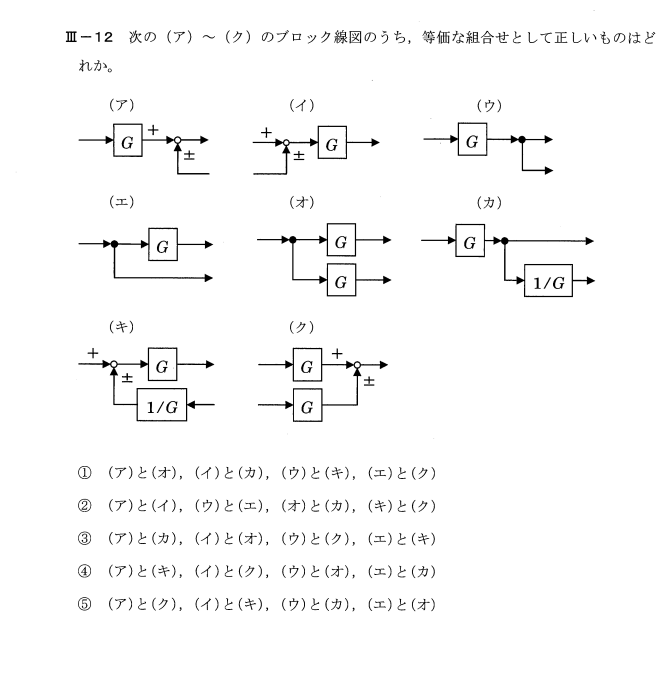
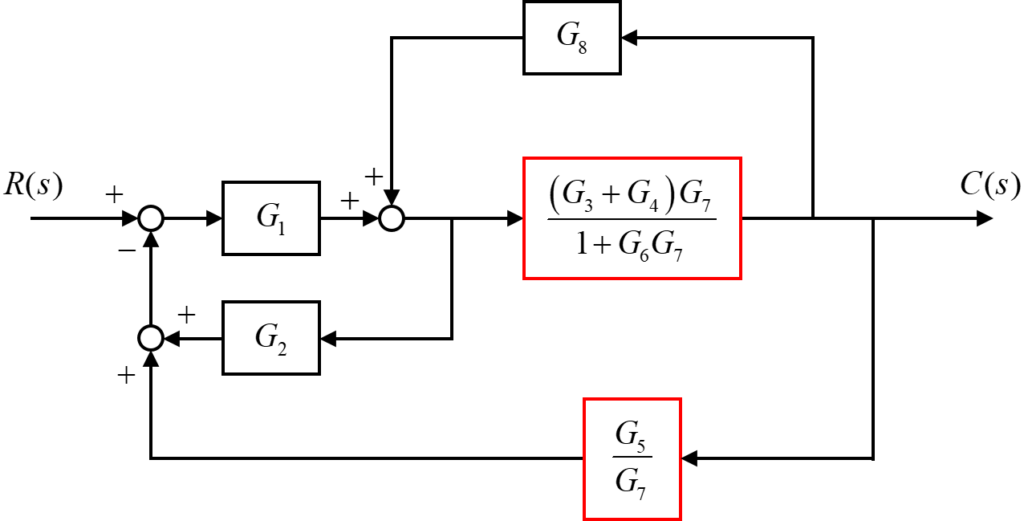
ブロック 線 図 簡略 化. ブロック線図を簡単化するには,目標値から出力までの伝達関数を求めてしまいます. まずは左辺に出力\(y\)を置きます. $$ y= $$ 右辺にはブロック線図の左側から順番に計算式を書いていきます. pidの例の場合は,まず目標値\(r\)と出力\(y\)の差をとっています. 問題図2.6 (b) (−1( ) +) −+ ( ) ( ) ( ) 図3: ブロック線図縮小規則を使用して、このブロック線図を簡略化(縮小)しましょう。 step 1 −ブロック$ g_1 $および$ g_2 $にはルール1を使用します。 ブロック$ g_3 $および$ g_4 $にはルール2を使用します。
があることを示唆している.事実,ブロックの簡略 化や詳細部の省略による伝達関数の低次元化が提案 されており,実際のサーボ系システムにおいて,制 最も簡略化された1次系の制御理論で十分であると いうことからも裏付けられる[1]. 高次の制御系を1次として近似する場合,制御定. ブロック線図は必要に応じて単純化しよう ほとんどの場合、ブロック線図はシステムの構成を直感的に分かりやすく表現するために使用します。 その場合は細かい部分をゴチャゴチャ描くよりも、 ブロックを単純化して全体をシンプルに表現したほうがよいでしょう 。 問題図2.6 (a) ( ) + − + −) − ( ) − − + 図2:
簡略化されたモデルに残っている極と零点は、赤色の x および o でマークされています。 元のモデルと簡略化されたモデルの周波数応答を観察しながら、異なる簡略化の許容誤差を試します。アプリケーションにとって重要な周波数範囲内のシステム動作を. そのため、与えられたブロック線図に対して簡略化を行うことで、入力信号\(r(s)\)に対する出力信号\(c(s)\)の関係を1つの伝達要素\(t(s)\) $$ t(s) = \frac{c(s)}{r(s)} $$ で表していきたいと思います。 ブロック線図を簡略化を行う方法には大きく2つの方法があります。 図2.15 dc サーボモータのブロック線図の簡略化 フィードバック結合 11 ブロックの 入れ替え 等価変換 変換前 変換後 表2.3 ブロック線図の等価変換 加え合せ点の 入れ替え 引き出し点の 入れ替え ブロックと 加え合せ点の 入れ替え(1) 等価変換 変換前 変換後 ブロックと 加え合せ点の 入.
但し、t は時定数)とする。図示の変位制御系が高応答であれ ば、トルク指令を無視してブロック線図 を変形すると、 足首トルクまでの伝達関数gは、数1の様になる。 【0019】 【数1】 【0020】数1において、kmkf>>1ならば、上 記伝達関数は、数2の式に近似される. 問題図2.6(a) ここでブロックと加え合わせ点の入れ替えを行うと, s (s+1)2 + 1 + − − r k y k s 図2: 【解答】 s (s+1)2 1 + + − − r k y 図1:
ただし,ブロック線図の簡略化の過程を図で示すこと。 問題図2.6 (a)~(c) のブロック線図を簡単化し,r か らy までの伝達関数を求めよ。 1 ( +1)2 + + − − 図1:

ブロック線図を簡略化する:ブロック線図の特性を利用する方法|Tajima Robotics
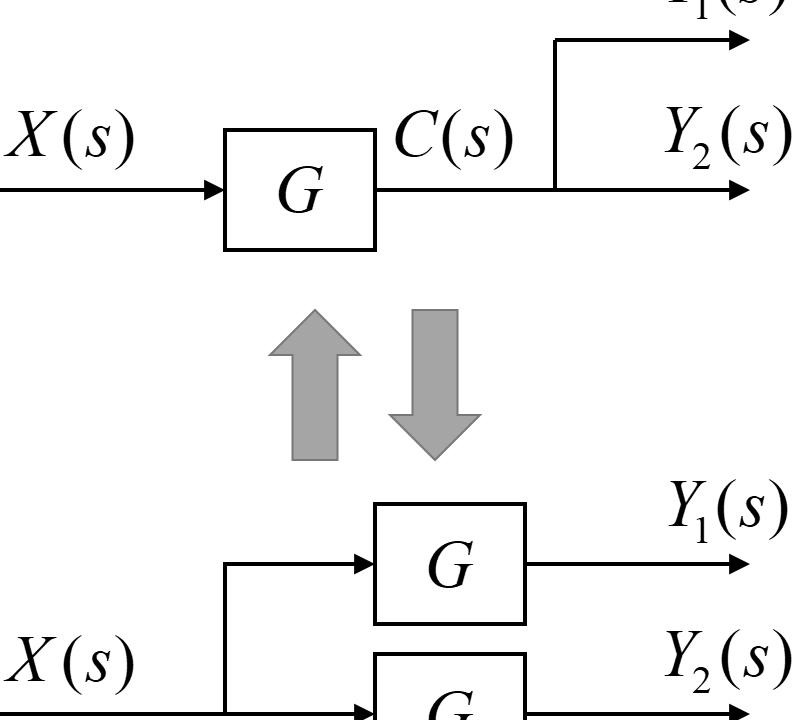
ブロック線図の簡単化(その3)|Tajima Robotics
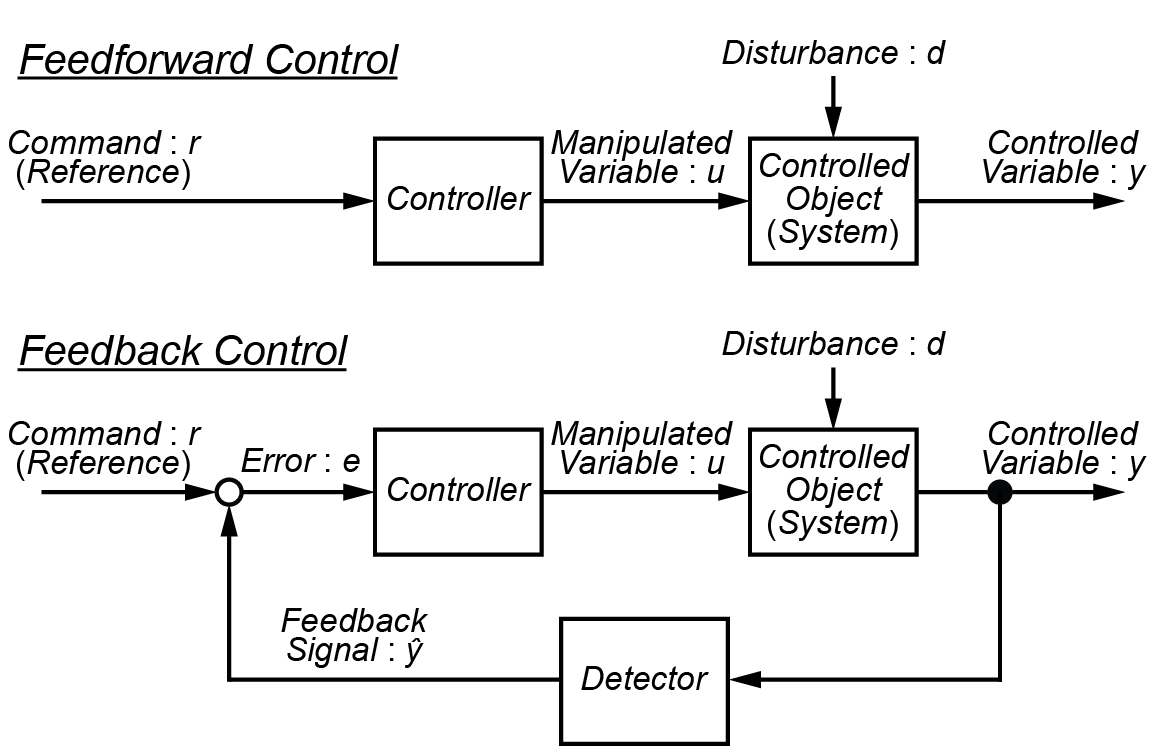
フィードフォワード制御とフィードバック制御でロボットを自由に制御しよう|Tajima Robotics